Nonlinear regression tutorial
By Abby Hudak
When relationships between variables is not linear you can try:
- transforming data to linearize the relationship
- fit non-linear functions to data (use nls example)
- fit polynomial or spline models to data (use growthrates package example)
linear regression: dependent variable = constant + parameter x indepenent variable + p x IV +....
y = B0 + B1X1 + B2X2 + ...
This doesn't mean you can't fit a curve! What makes it linear is that parameters are linear. You may have nonlinear independent variables ex) y = B0 +B1X1 +B2X(2)1. Instead of exponentially changing the independent variable, you could have log or inverse terms, etc.
nonlinear regression: Anything else. Can be crazy stuff like: B1 x cos(X+B4) + B2 x cos(2*X+B4)+B3. This makes it important that you do research to understand what functional form your data may take.
Nonlinear least squares approach
Nonlinear least squares is a good way to estimate parameters to fit nonlinear data. Uses a linear function to estimate a nonlinear one and iteratively works to find best parameter values.
1#simulate some data
2#set random number generator
3set.seed(2019)
4x<-seq(0,50,1)
5y<-((runif(1,10,20)*x)/(runif(1,0,10)+x))+rnorm(51,0,1)
6#for simple models nls find good starting values for the parameters even if it throws a warning
7
8#Michaelis-Menten equation
9m<-nls(y~a*x/(b+x))
10
11## Warning in nls(y ~ a * x/(b + x)): No starting values specified for some parameters.
12## Initializing 'a', 'b' to '1.'.
13## Consider specifying 'start' or using a selfStart model
14
15m
16
17## Nonlinear regression model
18## model: y ~ a * x/(b + x)
19## data: parent.frame()
20## a b
21## 17.908 7.645
22## residual sum-of-squares: 51.78
23##
24## Number of iterations to convergence: 6
25## Achieved convergence tolerance: 1.077e-06
26
27#will throw warning, but should work
28#get some estimation of goodness of fit
29cor(y,predict(m))
30
31## [1] 0.9658715
32
33#plot
34plot(x,y)
35lines(x,predict(m),col="red",lwd=3)
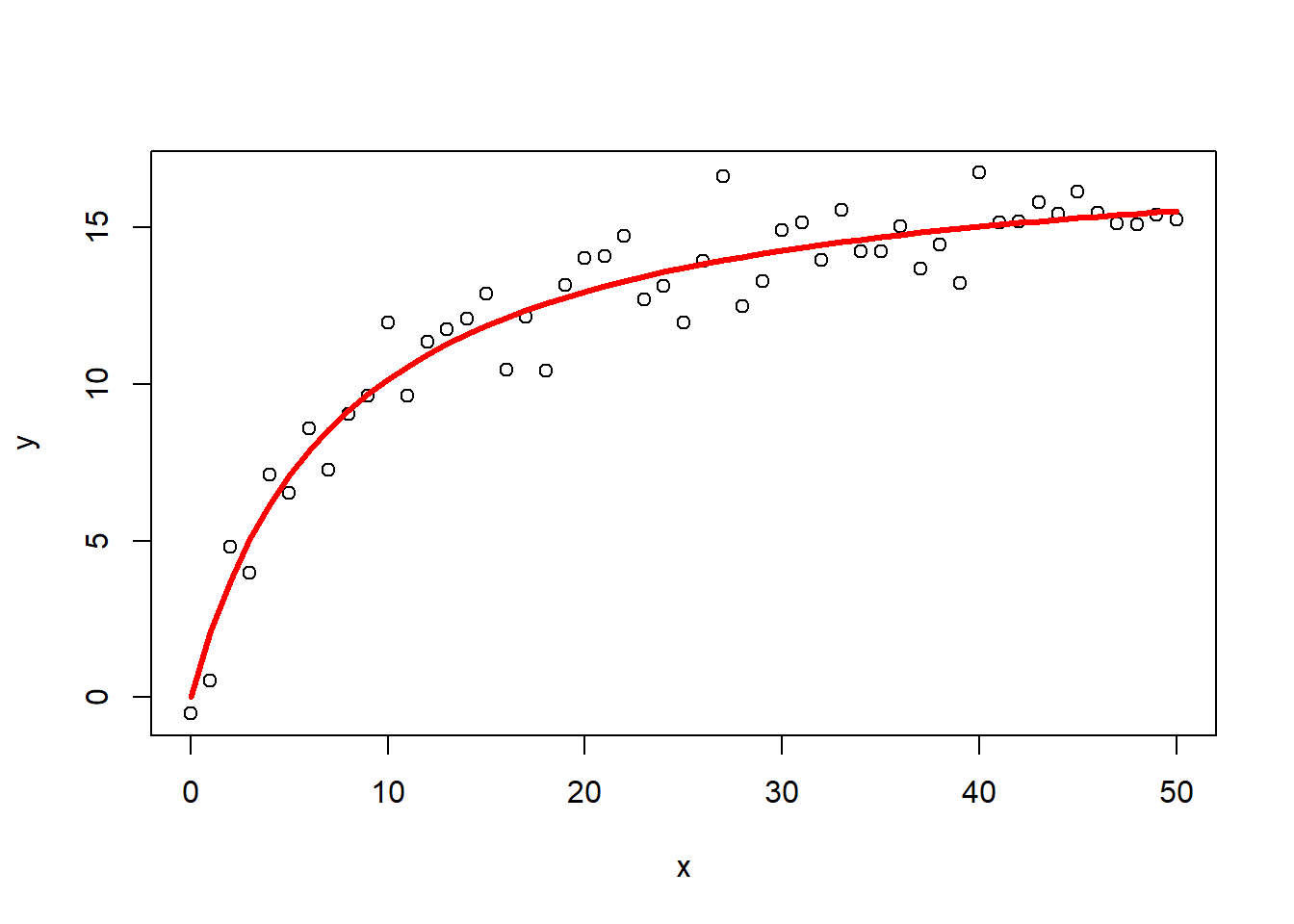
1#simulate some data, this without a priori knowledge of the parameter value
2x<-seq(0,50,1)
3y<-runif(1,5,15)*exp(-runif(1,0.01,0.05)*x)+rnorm(51,0,0.5)
4#visually estimate some starting parameter values
5plot(x,y)
6
7#from this graph set approximate starting values
8a_start<-8 #param a is the y value when x=0
9b_start<-log(0.1)/(50*8) #b is the decay rate. k=log(A)/(A(intial)*t)
10
11#model
12m1<-nls(y~a*exp(-b*x),start=list(a=a_start,b=b_start))
13m1
14
15## Nonlinear regression model
16## model: y ~ a * exp(-b * x)
17## data: parent.frame()
18## a b
19## 8.59328 0.03544
20## residual sum-of-squares: 7.588
21##
22## Number of iterations to convergence: 6
23## Achieved convergence tolerance: 7.615e-07
24
25#get some estimation of goodness of fit (should be closer to 1)
26cor(y,predict(m1))
27
28## [1] 0.9833285
29
30#plot the fit
31lines(x,predict(m1),col="red",lty=2,lwd=3)
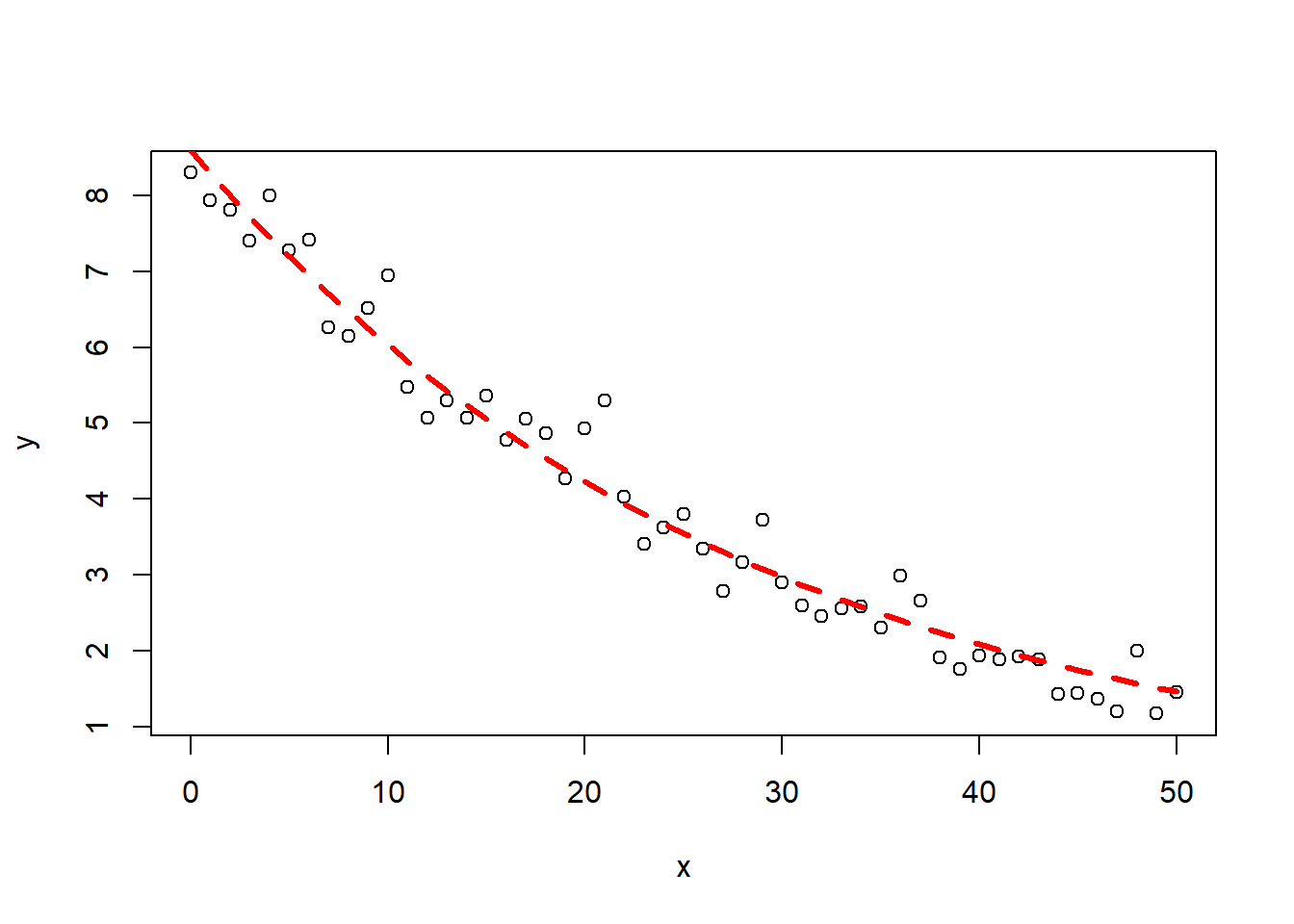
using differential equations
1library(deSolve) #this package is good for solving differential equations
2#simulating some population growth from the logistic equation and estimating the parameters using nls
3
4#defining a function
5log_growth <- function(Time, State, Pars) {
6 with(as.list(c(State, Pars)), {
7 dN <- R*N*(1-N/K)
8 return(list(c(dN)))
9 })
10}
11#Time is the time intervals, States are the variable names, Pars and parameters
12
13#pars, N_int, tmes are used to simulate data
14pars <- c(R=0.2,K=1000) #the parameters for the logisitc growth
15N_ini <- c(N=1) #the initial numbers
16times <- seq(0, 50, by = 1) #the time step to evaluate
17
18#the ODE (ordinary differential equation)
19out <- ode(N_ini, times, log_growth, pars)
20plot(out)

1#add some random variation to it
2N_obs<-out[,2]+rnorm(51,0,50)
3#remove numbers less than 1
4N_obs<-ifelse(N_obs<1,1,N_obs)
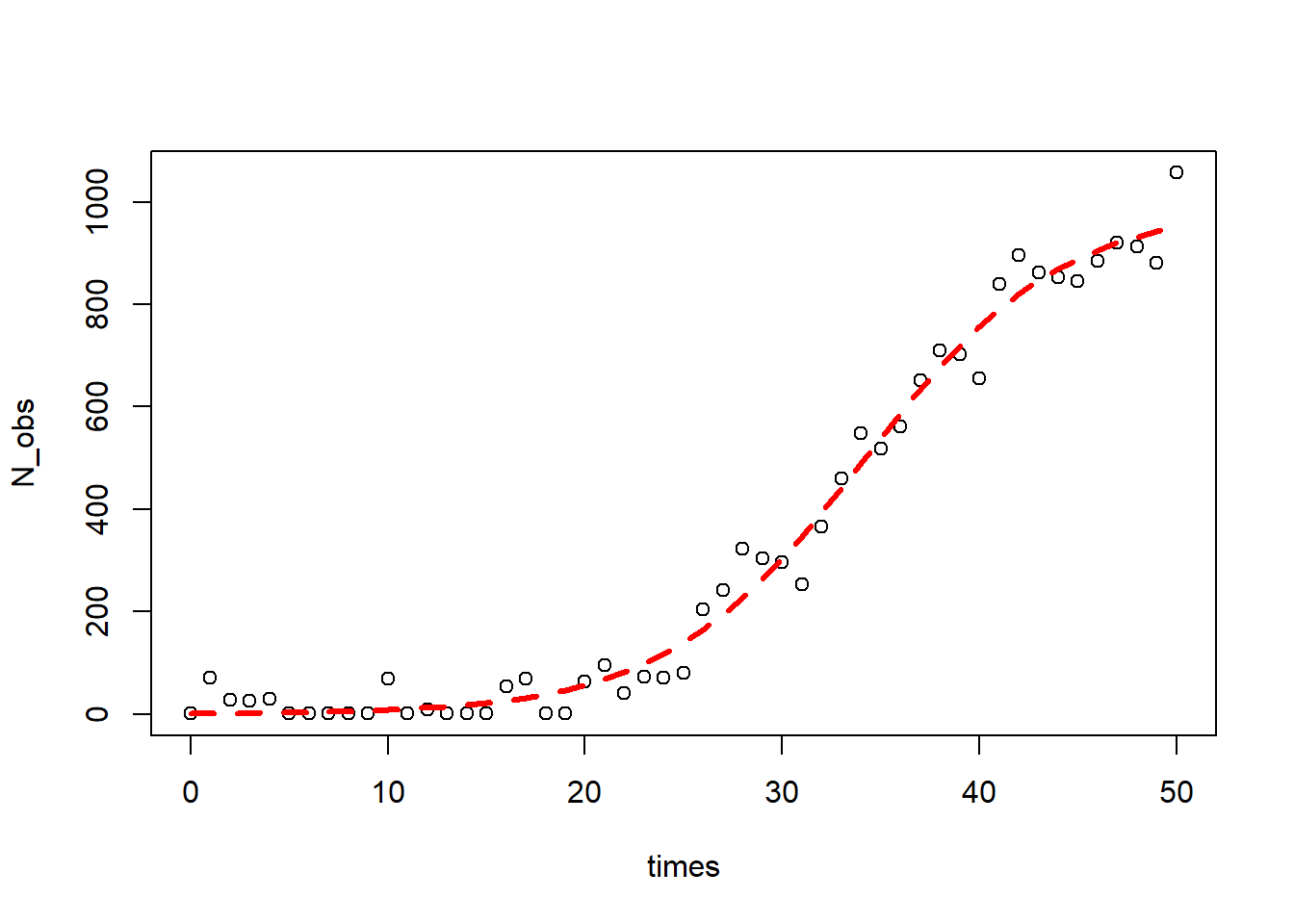
5#plot
6plot(times,N_obs)
7
8#Not having starting values only works sometimes with simple data and functions like in the first example.
9#notice how m3 WON'T work.Remember nls iteritavely runs to converge and this will not converge in under 30 iterations
10#m3<-nls(N_obs~K*N0*exp(R*times)/(K+N0*(exp(R*times)-1)))
11
12#getInitial gives guesses on parameter values based on data
13#SSlogis is a selfStarting model
14SS<-getInitial(N_obs~SSlogis(times,alpha,xmid,scale),data=data.frame(N_obs=N_obs,times=times))
15#follows this equation: N(t)=alpha/(1+e+((xmid-t)/scale)
16SS
17
18## alpha xmid scale
19## 991.798725 34.112932 5.045119
20
21#need to do some algebra to get parameterization right
22#we used a different parametrization
23K_start<-SS["alpha"]
24R_start<-1/SS["scale"]
25N0_start<-SS["alpha"]/(exp(SS["xmid"]/SS["scale"])+1)
26#the formula (not set up as differential equation) for the model
27log_formula<-formula(N_obs~K*N0*exp(R*times)/(K+N0*(exp(R*times)-1)))
28
29#fit the model
30m4<-nls(log_formula,start=list(K=K_start,R=R_start,N0=N0_start))
31
32#estimated parameters
33summary(m4)
34
35##
36## Formula: N_obs ~ K * N0 * exp(R * times)/(K + N0 * (exp(R * times) - 1))
37##
38## Parameters:
39## Estimate Std. Error t value Pr(>|t|)
40## K.alpha 991.79872 29.86851 33.205 <2e-16 ***
41## R.scale 0.19821 0.01338 14.817 <2e-16 ***
42## N0.alpha 1.14659 0.47931 2.392 0.0207 *
43## ---
44## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
45##
46## Residual standard error: 44.08 on 48 degrees of freedom
47##
48## Number of iterations to convergence: 0
49## Achieved convergence tolerance: 4.177e-06
50
51#get some estimation of goodness of fit (should be closer to 1)
52cor(N_obs,predict(m4))
53
54## [1] 0.9925536
55
56#plot
57lines(times,predict(m4),col="red",lty=2,lwd=3)
Maximum likelihood approach see nlme package. A bit more powerful and reliable method than nls.
growthrates package Finding best fit was a bit annoying for fitting a somewhat simple function. Fit a spline! A spline doesn't just make a line through data, it actually goes through each data point and fits a cubic ploynomial between two points. So the spline is a piecewise snapshot of the best fit. Allows for good interpolation.
function fit_spline fits a spline to just one and solves the cubic system of equations.
These youtube videos explain the calculus and concepts well: https://www.youtube.com/watch?v=BqZXS3n75l0
1library(growthrates)
2
3time<-rep(1:25, 8)
4y<-grow_logistic(time, c(y0=0.2, mumax=0.3, K=4))[,"y"]
5y<-jitter(y, factor=1, amount=0.3)
6data<-data.frame(cbind(time,y))
7data<-data[order(data$y),]
8data$ID<-c(rep(1:10,20))
9plot(time,y)

1splitted.data <- multisplit(data, c("ID"))
2
3## show which experiments are in splitted.data
4names(splitted.data)
5
6## [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
7
8## get table from single individual. Or could be an experiment, or batch, or block, etc.
9dat <- splitted.data[["1"]]
10dat[1, 2] = 0.03
11
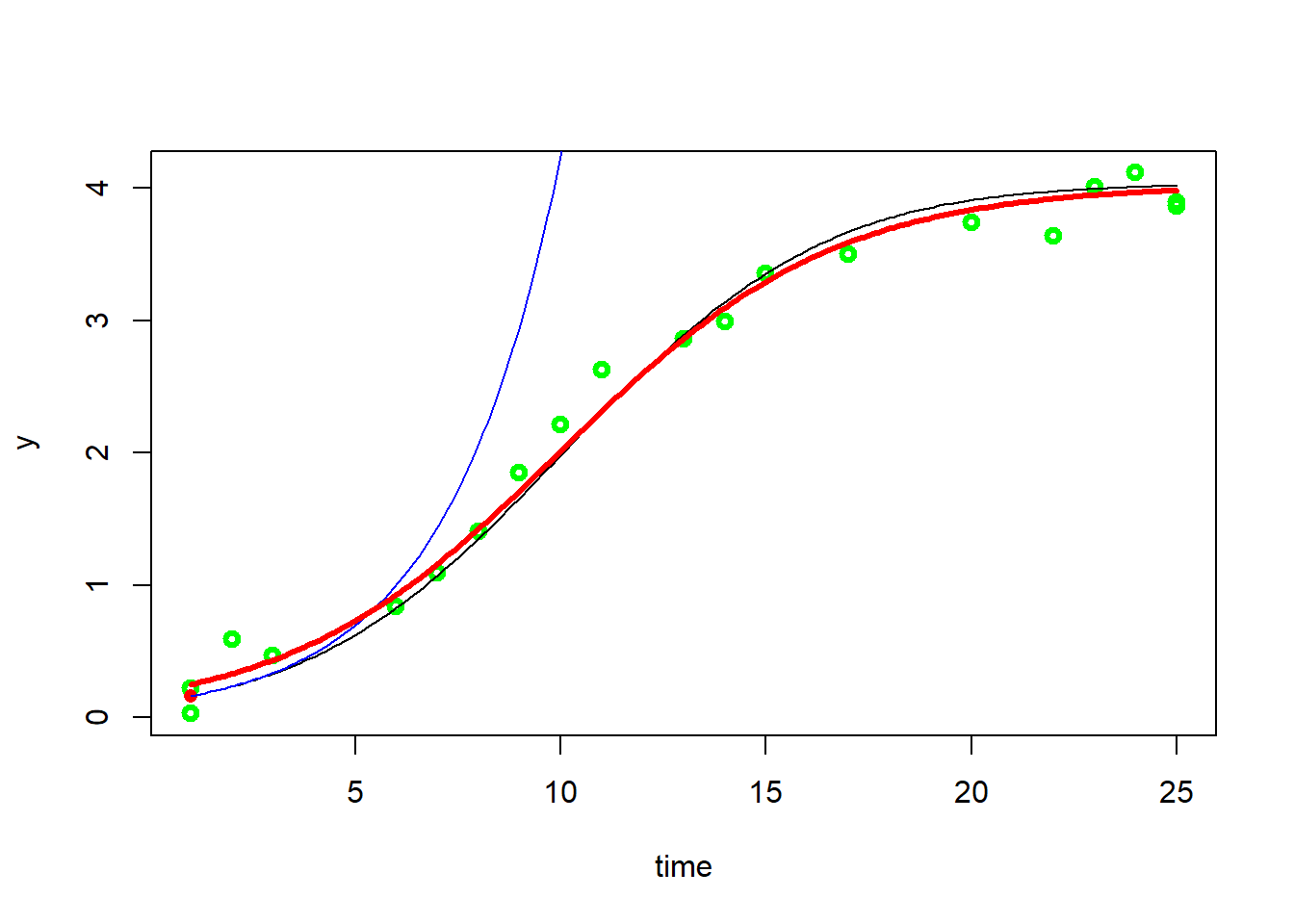
12fit0 <- fit_spline(dat$time, dat$y)
13plot(fit0, col="green", lwd=3)
14summary(fit0)
15
16## Fitted smoothing spline:
17## Call:
18## smooth.spline(x = time, y = ylog)
19##
20## Smoothing Parameter spar= 0.6721364 lambda= 0.006882113 (12 iterations)
21## Equivalent Degrees of Freedom (Df): 3.685259
22## Penalized Criterion (RSS): 2.029662
23## GCV: 0.3015
24##
25## Parameter values of exponential growth curve:
26## Maximum growth at x= 1.001382 , y= 0.1644875
27## y0 = 0.1145593
28## mumax = 0.3612431
29##
30## r2 of log transformed data= 0.8652797
31
32#can get maximum growth rate from here. Plot will show the exponetial curve (blue line) from max rate
33
34## initial parameters
35p <- c(coef(fit0), K = max(dat$y))
36
37## avoid negative parameters
38lower = c(y0 = 0, mumax = 0, K = 0)
39
40fit3<-fit_growthmodel(grow_logistic, p=p, time=data$time, y=data$y)
41lines(fit3, col="red", lwd=3)
1summary(fit3)
2
3##
4## Parameters:
5## Estimate Std. Error t value Pr(>|t|)
6## y0 0.188670 0.012562 15.02 <2e-16 ***
7## mumax 0.301080 0.007458 40.37 <2e-16 ***
8## K 4.027982 0.029659 135.81 <2e-16 ***
9## ---
10## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
11##
12## Residual standard error: 0.1713 on 197 degrees of freedom
13##
14## Parameter correlation:
15## y0 mumax K
16## y0 1.0000 -0.9448 0.5116
17## mumax -0.9448 1.0000 -0.6615
18## K 0.5116 -0.6615 1.0000
19
20#Get parameters for the entire population
21
22fit4<-all_growthmodels(
23 y ~ grow_logistic(time, parms) | ID,
24 data = data, p = p, lower = lower) #gives parameters for each individual
25
26results(fit4, extended=TRUE) #extended gives you time estimates of saturation values.
27
28## ID y0 mumax K turnpoint sat1 sat2 sat3
29## 1 1 0.1775788 0.3186817 3.922830 9.567004 13.69952 15.84286 18.80644
30## 2 2 0.2131942 0.2973178 3.962413 9.643233 14.07267 16.37004 19.54655
31## 3 3 0.1958260 0.2873056 4.118416 10.432393 15.01620 17.39362 20.68083
32## 4 4 0.1639432 0.3095515 4.076656 10.248580 14.50299 16.70954 19.76054
33## 5 5 0.1514473 0.3280776 3.963867 9.832374 13.84654 15.92849 18.80720
34## 6 6 0.1988192 0.2916016 4.077459 10.188041 14.70430 17.04671 20.28550
35## 7 7 0.2349602 0.2860918 4.040224 9.733663 14.33695 16.72443 20.02562
36## 8 8 0.1929363 0.2827270 4.130590 10.667467 15.32552 17.74143 21.08189
37## 9 9 0.1830012 0.3046824 4.035454 10.000489 14.32289 16.56470 19.66445
38## 10 10 0.1680191 0.3139180 4.027611 9.984249 14.17949 16.35534 19.36390
39## r2
40## 1 0.9896373
41## 2 0.9803218
42## 3 0.9865337
43## 4 0.9893162
44## 5 0.9840925
45## 6 0.9897703
46## 7 0.9846571
47## 8 0.9887043
48## 9 0.9836142
49## 10 0.9825879
How ID is set right now, you will get parameter estimates for each individual. May change ID to treatment, experiment, block, etc. based on your data. If you replace it with treatment, you will get the parameters for each treatment. May include more by adding a plus sign between them.
Parameters: y0=initial y value; mumax=intrinsic growth rate; K=asymptotic size
Saturation times: turnpoint=time of turnpoint (50% saturation); sat1=time of minimum of 2nd derivative (minimum growth rate); sat2=time of intercept between steepest increase (tangent of mumax) and K; sat3=time when asymptotic size is reached
This showed how to fit logistic equations, but this package fits lots of different curves!
If you are more interested in defining more complex forumlas and defining their log-liklihood functions, I recommend the package bblme and use the function mle2